
| Electromagnetic theory (AS.171.603)
(AKA Defense against the dark arts of quantum mechanics) Nadia Zakamska Spring 2021 |
| This is an old course webpage for information only, not a currently active course. Some materials have been removed in preparation for the next class. |
| Spring 2021 Remote Instruction: Frequently Asked Questions |
This course will be taught in the remote / synchronous mode. It will be desirable to attend in real time so that we can discuss any questions that arise. However, it is not required to attend in real time. All meetings will be recorded, and students can go over them on their own time. This class can be taken fully synchronously, fully asynchronously or in between.
The lectures will likely take place at the times specified on the SIS (M/F at 1:30 pm Baltimore time); however, I will circulate a poll to see if there is a more convenient time. Lectures will be synchronous (meaning I will give them in real time, not pre-record), but they will be recorded and posted for later viewing.
The TA for this course is Chris Lygouras. There is currently no plan for regular sections or for regular office hours either for Nadia Zakamska or for Chris Lygouras. The students are strongly encouraged to form study groups (see homework policy below on the scope of the allowed collaboration). However, based on previous years' experiences, I am considering organizing a couple of sections in the beginning of the semester to assist with the first two HW assignments. I will poll students in the beginning of the semester and determine the need and schedule for any sections. The sections will also be synchronous and recorded for later access.
The graded content of the class includes homework assignments (one every two weeks, 6-7 assignments are expected) and the final exam. All assignments will be submitted through Gradescope. The final exam will be asynchronous. I will give a 24-hour (or longer) window (date TBD by mutual agreement and the registrar's exam schedule) when the exam will be open on Gradescope.
All materials for the class will be on this webpage, in the OneDrive folder accessible by all registered students, and on Gradescope. There is no BlackBoard page for this course. If you cannot access the OneDrive folder, email NLZ. Zoom access codes will be posted in the "announcements" file in OneDrive. Gradescope access code will be posted in the same place. I will regularly use the class email address for communicating with the class.
If you are an undergraduate interested in taking the course, please email NLZ. This course is not a high-level version of the undergraduate course 171.301; it assumes strong familiarity with Griffiths (171.301) and contains qualitatively new material. Therefore, it is not a suitable replacement for 171.301.
| Course information |

1. Overview
This is a graduate course that covers relativistic particle dynamics, the fundamentals of classical field theory, radiation and propagation of electromagnetic waves, and Maxwell's equations in static and dynamic applications. Furthermore, we will discuss advanced topics in electrodynamics in medium and in plasmas and topics in current research. We will introduce analytical methods of EM theory (tensor calculus, PDEs and Green's functions and basis functions in several geometries, and linear stability analysis) and occasionally use scientific computing and visualization software for numerical calculations. The goal of the class is to equip students with foundations and tools necessary to read scientific literature and to conduct research projects in graduate-level physics.
2. Lecture schedule
Instructor: Prof. Nadia Zakamska
Lectures: Mon and Fri, 1:30 - 2:45 pm (tentatively); office hours: by appointment.
TA / grader: Chris Lygouras
3. Homework and grading
(1) There will be roughly one homework every four lectures. You may discuss homework with your classmates or others. You may not look at their written solutions (and thus, you may not show yours to others). Discussion and study groups are strongly encouraged; however, direct copying of assignments will be considered a serious violation of the homework policy. Please report any violations to the instructor.
(2) You may use Internet, books, journals, and departmental resources and software. Google is an excellent place to start if there are terms and abbreviations you don't know. If you use a webpage or an article in your final solution, please provide a reference. If you use a direct quote, you must put it in quotation marks and provide a reference. Your own words are always preferable.
(3) Unless specified otherwise, there is no need to type your solutions, but we need to be able to read your handwriting.
(4) Homework due dates and times will be posted on Gradescope. Gradescope automatically tracks late submissions.
(5) Everybody gets one free pass (per the entire semester) on one <=24 hour delay on an assignment. Aside from this, submissions late by 0-24 hours suffer a 50% penalty. Submissions late by 24 hours or more will suffer 100% penalty.
(6) No communication with other humans in any form will be allowed during the final exam. Final exam will be open book / open everything.
The final grade is 1/2 homework, 1/2 final exam. From past experience, it is likely that the passing grade is over 50%. Therefore, it is not possible to pass the class without submitting homework.
The strength of the university depends on academic and personal integrity. In this course, you must be honest and truthful. Ethical violations include cheating on exams, plagiarism, reuse of assignments, improper use of the Internet and electronic devices, unauthorized collaboration, alteration of graded assignments, forgery and falsification, lying, facilitating academic dishonesty, and unfair competition. The guidelines for this course are listed above. Report any violations you witness to the instructor. You may consult the associate dean of student conduct (or designee) by calling the Office of the Dean of Students at 410-516-8208 or via email at [email protected]. For more information, see the Homewood Student Affairs site on academic ethics.
4. Conventions
(1) A quick survey of the literature reveals that modern scientific convention (astrophysics, particle physics) is Greek indices for the 4D space-time and Latin indices for the 3D space.
(2) Since E and B transform into each other depending on the reference frame, "To measure E and B in different units is completely antithetical to the entire notion of relativistic invariance" (Melvin Schwartz). We will use the cgs system where E and B have the same units. We will discuss how to transform to other systems of units when necessary. In practice, PhD level physicists need to know both systems of units, plus additional field-specific systems. For example, most undergraduate physics teaching (and of course all engineering-related teaching) is in MKS, most graduate teaching is in cgs or other field-specific units, and research papers use unit systems interchangeably depending on the conventions of the field.
(3) As a physicist, you may need to do order-of-magnitude estimates of various physical effects. To this end, you must carry around in your head some fundamental constants of nature. This is a list of constants that students will find useful to know. These values can and do come up during questioning at the research exams, the GBOs, the thesis defenses and in your professional presentations.
5. Topics and textbooks
A list of textbooks, some PDF notes and links to pedagogical materials will be available in the OneDrive folder.
This course will not follow the standard Jackson syllabus (although there will be some overlap with Jackson). This is, roughly, the list of physics topics and the relevant mathematical apparatus we will discuss:
Part 1: Relativistic dynamics, 3D and 4D tensor calculus
Part 2: Classical field theory
Part 3: Electrostatics / magnetostatics, special functions in various geometries, Green's functions
Part 4: Generation and propagation of radiation in vacuum [am trying to squeeze in advanced wave optics, if we have time]
Part 5: Propagation of radiation in media, dynamics of plasmas / dispersion relations, linear stability analysis.
Parts 1, 2 and 4 are loosely based on Landau and Lifshitz volume 2 ("The classical theory of fields"). In terms of scope, we will cover their chapters 1-9 and in roughly the same order (although with less 4D formalism). Unfortunately, their index notation is different from ours (Latin instead of Greek for 4D) and there are few, if any, pedagogically useful exercises, so these will be coming from elsewhere.
Another useful source which gives some of the material in our Parts 1-2, but in a more accessible vector form and with more detailed derivations, is A.S.Kompaneyets ("Theoretical physics").
Textbook on Special Relativity by N. Zakamska, we will review material in Chapters 1-6 (undergraduate level) and introduce material in Chapters 7-8 (graduate level)
Part 3 will cover some of the material in Chapters 1-5 of Jackson's "Electrodynamics".
Part 5 is typically covered in advanced graduate plasma physics courses. I'll provide some notes and references.
We will also discss topics related to modern research and modern analysis tools.
6. Software and resources for the remote mode in Spring 2021
All course information will be in the class OneDrive folder. I have to enable person-by-person access. If you do not have the link to the OneDrive folder and / or you cannot access it, this means that you registered after I last checked the roster. Email NLZ for access.
Please check the OneDrive folder for Zoom information.
All course video materials and textbook information will be available there.
All homeworks and exams will be through Gradescope. Access code for Gradescope is in the "announcements" in the OneDrive folder.
Software policy (AKA what to do if technoogy goes sideways) is available here. Please be conscious of the fact that this is a large class (the largest 603 we have had in many years). We ask everybody for their best efforts in time management, so that the instructors have as few exceptions to deal with as possible.
| Assignments |

Assignments will be posted on Gradescope, and after they are graded and returned, both assignments and solutions will be posted in OneDrive.
Homework 1 is posted to Gradescope, due Feb 8 before the lecture. Assignments will be due every two weeks, with allowances made for the University spring break days.
| Syllabus |

[References: LL - Landau Lifschitz with section numbers; NZ -- arXiv:1511.02121 with chapter numbers; AK - Kompaneyets with chapter numbers; JDJ - Jackson with chapter numbers; BT -- Binney and Tremaine with chapter numbers]
-- Part 1. Relativistic kinematics and dynamics
Jan 25. Lecture 1. Einstein's principle of relativity. Derivation of the Lorentz transform in a variety of ways. Refresher on standard applications of the Lorentz transforms: time dilation, length contraction. [LL 1-4; NZ 1-3]
Jan 29. Lecture 2. Tensor calculus in 3D.
Feb 1. Lecture 3. Kronecker symbols and anti-symmetric symbols. 4D invariants. Velocity transforms.
Feb 3. Section 1. 3D tensor calculus, special relativity.
Feb 5. Lecture 4. Tensor calculus in 4D, contravariant and covariant 4-vectors. 4-vectors of velocity, acceleration, energy, momentum, charge density. [LL 5-7, 9; NZ 5-7]
Feb 8. Lecture 5. Dynamics of relativistic particles. Motion in constant EM fields.
Feb 12. Lecture 6. Tensor of electromagnetic fields. Field transformations. [LL 6; NZ 7-8]
Feb 15. Lecture 7. Field invariants. [LL 23-25; NZ 8; JDJ 12] Probability density distributions and law of unconscious statistician. [LL 10, 11 and Wikipedia page]
Feb 17. Section 2. 4D tensors, relativistic particle dynamics.
-- Part 2. Classical field theory
Feb 19. Lecture 8. Scalar and vector potentials, charge conservation. Maxwell's equations in differential form.
Feb 22. Lecture 9. 4-potentials. Gauge invariance. Fields of moving charge. Maxwell's equations in covariant form. [AK 12; LL 18, 19, 26, 30; JDJ 12; Wikipedia covariant formulation is a really nice summary, despite MKS and a different sign definition in the Maxwell 3D stress tensor from the one we used].
Feb 26. Lecture 10. Maxwell stress tensor (3D), energy-momentum tensor (4D) [LL 31, 32, 33]
March 1. Lecture 11. Lagrangian for particles [LL 16, 17, AK 21], Lagrangian for fields [AK 13; LL 27, 32]
-- Part 3. Static solutions of Maxwell's equations
March 5. Lecture 12. Poisson and Laplace equation for fields and for the scalar and vector potentials and its Green's functions. [JDJ 1.1-1.7, 5.1-5.5]
March 8. Lecture 13. Multipole expansion [LL 40-44; JDJ 4.1-4.2, 5.6]
March 12. Lecture 14. Neumann and Dirichlet boundary conditions [JDJ 1.9], reducing Poisson equation to an ODE in orthogonal coordinate systems.
March 15. Lecture 15. Numerical methods [JDJ 1.13], general solution to Poisson equation through Green's functions [JDJ 1.7-1.10], separation of variables in Cartesian coordinates [JDJ 2.9]
March 19. Lecture 16. Separation of variables in cylindrical coordinates [JDJ 3.7, 3.8, 3.11]
March 22. Spring break.
March 26. Lecture 17. Potential of a charged disk [BT 2], separation of variables in spherical coordinates [BT 2, Appendix], CMB power spectrum analysis.
-- Part 4. Dynamic solutions of Maxwell's equations in vacuum.
March 29. Lecture 18. EM waves in vacuum. Tensor of polarization. [LL 46-50]
April 2. Lecture 19. Stokes parameters [Kosowsky astro-ph/9501045 and Wikipedia]. Spectral decomposition of intensity [LL 49]. Green's function for D'Alambert's equation [LL 62]
April 5. Lecture 20. Lienard-Wiechert potentials. Dipole radiation [LL 63, 66, 67]. Thomson scattering.
April 9. Lecture 21. Rayleigh scattering. Eddington limit. Multipole expansion for radiation.
April 12. Lecture 22. Cyclotron and Synchrotron emission.
-- Part 5. Topics in plasma physics and EM in media.
Flux freezing. E-cross-B drift.
April 16. Lecture 23. Drift of particles in Earth's magnetic field. Adiabatic invariant and magnetic mirrors. Dispersion of wave packets. Dispersion of EM waves in linear media.
April 19. Lecture 24. Dispersion of EM waves in cold plasma. Dispersion of EM waves in metals.
April 23. Lecture 25. Dispersion relation and optical properties of materials. Drude model.
April 26. Lecture 26. Kramers-Kroenig relations.
| Miscellaneous |
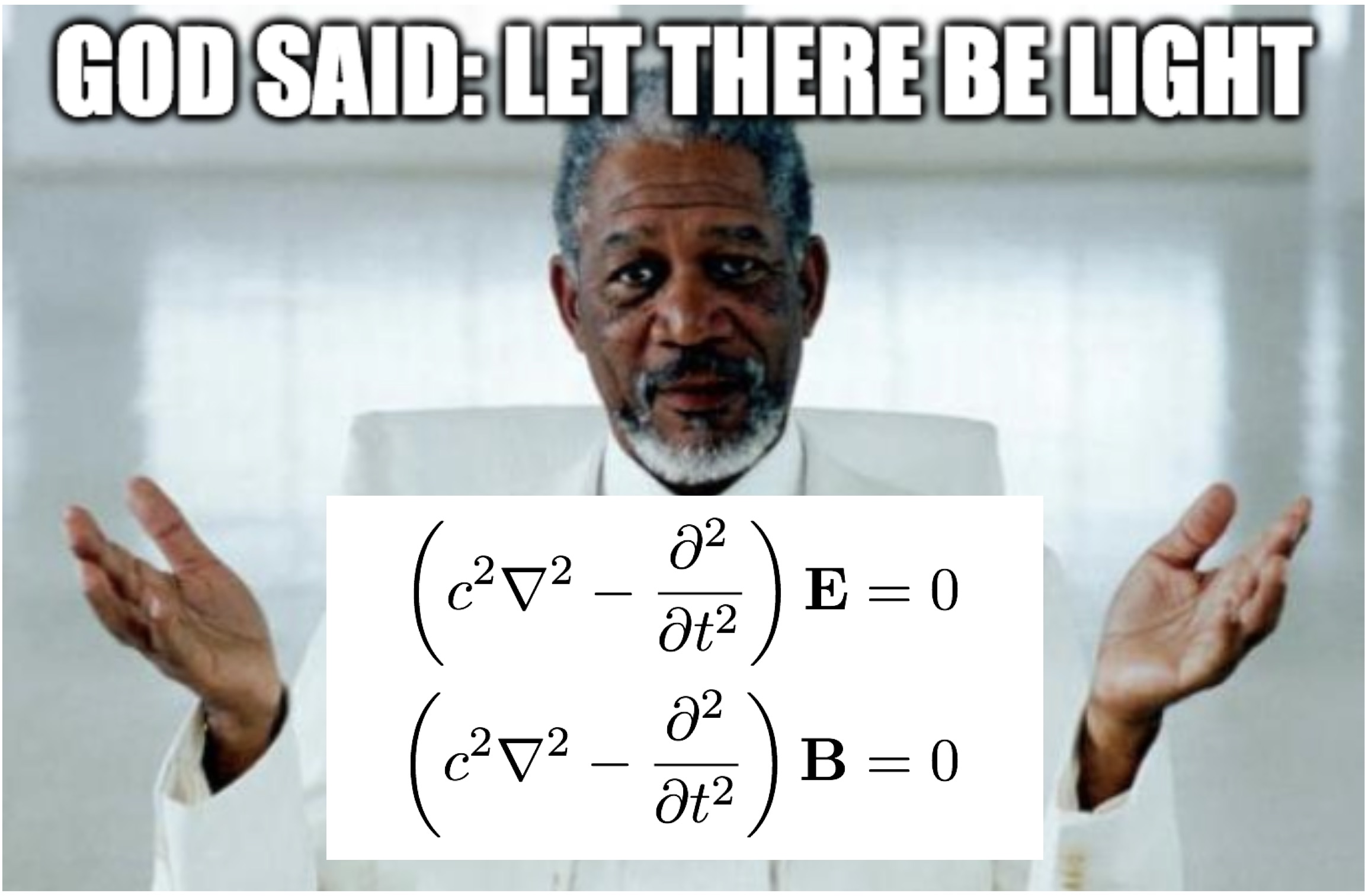
CGS vs MKS (scroll down for a conversion table for electromagnetic units)
Curvilinear systems (scroll down to the grey tables which are the most useful)
Latex template, style file and instructions
Garland -- Advice for beginning physics speakers